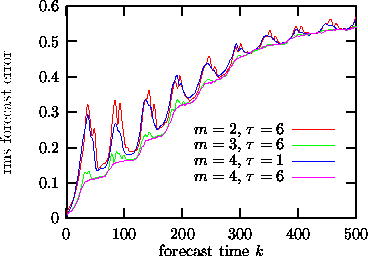
Figure: Predictions k time steps ahead (no iterated predictions) using the program zeroth. Top (red) curve: embedding dimension two is insufficient, since these flow data fill a (2+
Figure: Predictions k time steps ahead (no iterated predictions) using the program zeroth. Top (red) curve: embedding dimension two is insufficient, since these flow data fill a (2+)-dimensional attractor. Second from top (blue): Although embedding dimension four should in theory be a good embedding,
suppresses structure perpendicular to the diagonal so that the predictions are as bad as in m=2! Lower (green, pink) curves: m=3 and 4 with a delay of about 4-8 time units serve well.
Apart from the embedding parameters, all that has to be specified for zeroth order predictions is the size of the neighborhoods. Since the diffusive motion below the noise level cannot be predicted anyway, it makes sense to select neighborhoods which are at least as large as the noise level, maybe two or three times larger. For fairly clean time series, this guideline may result in neighborhoods with very few points. Therefore zeroth also permits to specify the minimal number of neighbors to base the predictions on.
A relevant modification of this method is to extend the neighborhood ![]() to infinity, but to introduce a distance dependent weight,
to infinity, but to introduce a distance dependent weight,
![]()
where w is called the kernel. For ![]() where
where ![]() is
the Heaviside step function, we return to Eq.(
is
the Heaviside step function, we return to Eq.(![]() ).
).