Highlights
Publication Highlights
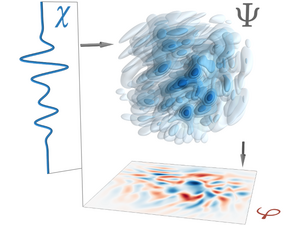
Bioenergetic costs and the evolution of noise regulation by microRNAs
MicroRNAs (miRNAs) are short strands of genetic material that regulate various cellular functions and developmental processes. One of the regulatory functions of miRNAs is noise control that confers robustness in gene expression. The interaction with their target messenger RNA (mRNA) requires a specific binding sequence of 6-8 nucleotide pairs in length. There are a variety of open questions about the evolution of miRNA regulation regarding their functional efficiency and binding specificity.
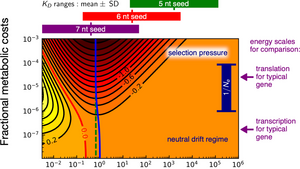
Efe Ilker of the Max Planck Institute for the Physics of Complex Systems and Michael Hinczewski (Case Western Reserve University) show that this regulation incurs a steep energetic price, so that natural selection may have driven such systems towards greater energy efficiency. This involves tuning the interaction strength between miRNAs and their target messenger RNAs, which is controlled by the length of a miRNA seed region that pairs with a complementary region on the target. They show for the first time that microRNAs lie in an evolutionary sweet spot that may explain why 7 nucleotide pair interactions are prevalent: sequences that are much longer or shorter would not have the right binding properties to reduce noise optimally. To achieve this, they develop a stochastic model of miRNA noise regulation, coupled with a detailed analysis of the associated metabolic costs and binding free energies for a wide range of miRNA seeds. Moreover, the behaviour of the optimal miRNA network mimicks the best possible linear noise filter, a classic concept in engineered communication systems. These results illustrate how selective pressure toward metabolic efficiency has potentially shaped a crucial regulatory pathway in eukaryotes.
E. Ilker and M. Hinczewski, Proc. Natl. Acad. Sci. USA 121, e2308796121 (2024)
Read moreEfe Ilker of the Max Planck Institute for the Physics of Complex Systems and Michael Hinczewski (Case Western Reserve University) show that this regulation incurs a steep energetic price, so that natural selection may have driven such systems towards greater energy efficiency. This involves tuning the interaction strength between miRNAs and their target messenger RNAs, which is controlled by the length of a miRNA seed region that pairs with a complementary region on the target. They show for the first time that microRNAs lie in an evolutionary sweet spot that may explain why 7 nucleotide pair interactions are prevalent: sequences that are much longer or shorter would not have the right binding properties to reduce noise optimally. To achieve this, they develop a stochastic model of miRNA noise regulation, coupled with a detailed analysis of the associated metabolic costs and binding free energies for a wide range of miRNA seeds. Moreover, the behaviour of the optimal miRNA network mimicks the best possible linear noise filter, a classic concept in engineered communication systems. These results illustrate how selective pressure toward metabolic efficiency has potentially shaped a crucial regulatory pathway in eukaryotes.
E. Ilker and M. Hinczewski, Proc. Natl. Acad. Sci. USA 121, e2308796121 (2024)
Publication Highlights
Characterising the gait of swimming microorganisms
The survival strategies of Escherichia Coli are controlled by their run-and-tumble "gait". While much is known about the molecular mechanisms of the bacterial motor, quantifying the motion of these microorganisms in three dimensions has remained challenging. Christina Kurzthaler of the Max Planck Institute for the Physics of Complex Systems and her collaborators have now proposed a high-throughput method, using differential dynamic microscopy and a renewal theory, for measuring the run-and-tumble behavior of a population of E. Coli cells. Besides providing a full spatiotemporal characterisation of their swimming gait, this new method allowed relating, for the first time, molecular properties of the motor to the dynamics of engineered E. coli cells. It therefore lays the foundation for future studies on gait-related phenomena in different microorganisms and has the potential of becoming a standard tool for rapidly determining motility parameters of swimming cells.
More details can be found in a press release (PDF).
C. Kurzthaler*, Y. Zhao*, N. Zhou, J. Schwarz-Linek, C. Devailly, J. Arlt, J.-D. Huang, W. C. K. Poon, T. Franosch, J. Tailleur, and V. A. Martinez, Phys. Rev. Lett. 132, 038302 (2024)
Y. Zhao*, C. Kurzthaler*, N. Zhou, J. Schwarz-Linek, C. Devailly, J. Arlt, J.-D. Huang, W. C. K. Poon, T. Franosch, V. A. Martinez, and J. Tailleur, Phys. Rev. E 109, 014612 (2024)
Selected for a Synposis in Physics.
Read moreMore details can be found in a press release (PDF).
C. Kurzthaler*, Y. Zhao*, N. Zhou, J. Schwarz-Linek, C. Devailly, J. Arlt, J.-D. Huang, W. C. K. Poon, T. Franosch, J. Tailleur, and V. A. Martinez, Phys. Rev. Lett. 132, 038302 (2024)
Y. Zhao*, C. Kurzthaler*, N. Zhou, J. Schwarz-Linek, C. Devailly, J. Arlt, J.-D. Huang, W. C. K. Poon, T. Franosch, V. A. Martinez, and J. Tailleur, Phys. Rev. E 109, 014612 (2024)
Selected for a Synposis in Physics.
Publication Highlights
Exotic fractons constraining electron motion to one dimension
Fractons are the latest addition to the set of exotic quasiparticles in condensed matter, and models exhibiting fracton phenomenology are highly sought after. Alexander Wietek of the Max Planck Institute for the Physics of Complex Systems and his collaborators have now proposed a model that shows this phenomenology. They studied a simple "doped" Ising magnet on the two-dimensional honeycomb lattice with anisotropic Ising couplings that exhibits a dipolar symmetry. This peculiar property leads to the complete localization of one hole, whereas a pair of two holes is localized only in one spatial dimension. The emergent dipole symmetry is found to be remarkably precise, being present up to the 15th order of perturbation theory and to numerically accurate precision away from the perturbative limit. The proposed model captures the very essence of subdimensional mobility constraints and could become a prime example of how new and exotic fracton-like quasiparticles can be implemented in a condensed matter setting.
Sambuddha Sanyal, Alexander Wietek, and John Sous, Phys. Rev. Lett. 132, 016701 (2024)
Read moreSambuddha Sanyal, Alexander Wietek, and John Sous, Phys. Rev. Lett. 132, 016701 (2024)
Publication Highlights
Using quantum computers to test Jarzynski’s equality for many interacting particles
Statistical mechanics is a branch of physics that uses statistical and probabilistic methods to understand the behaviour of large numbers of microscopic particles, such as atoms and molecules, in a system. Instead of focusing on the individual motion of each particle, statistical mechanics analyses the collective properties of the system. It provides a bridge between the microscopic world of particles and the macroscopic world that we can observe, explaining phenomena like the behaviour of liquids and gases, phase transitions, and the thermodynamic properties of materials. Through the statistical distribution of particle properties, such as energy and velocity, statistical mechanics helps us make predictions about how physical systems behave on a larger scale, contributing to our understanding of fundamental principles in physics and chemistry.
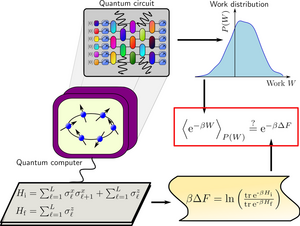
One of the most remarkable relations in statistical mechanics is Jarzynski's equality, connecting the irreversible work performed in an arbitrary thermodynamic process with the energy and entropy of the system in thermodynamic equilibrium. Because the system is free to leave the equilibrium state during its evolution, Jarzynski’s equality is a prime example of how equilibrium physics can constrain the outcome of nonequilibrium processes. Remarkably, the familiar Second Law of Thermodynamics – a fundamental principle of physics – follows directly from Jarzynski’s equality. The Second Law is a statement about the average properties of particles in a system undergoing a thermodynamic process, and postulates that heat always flows spontaneously from hotter to colder regions of the system. Intriguingly, Jarzynski’s equality shows that this fundamental law of Thermodynamics can be “violated” in individual realizations of a process (but never on average!).
Despite its fundamental importance, experimental tests of Jarzynski’s equality for classical and quantum systems are extremely challenging, since they require complete control in manipulating and measuring the system. Even more so, a test for many quantum interacting particles was until recently completely missing.
In a new joint study, an international team from the Max Planck Institute for the Physics of Complex Systems, the University of California at Berkeley, the Lawrence Berkeley National Laboratory, the German Cluster of Excellence ML4Q and the Universities of Cologne, Bonn, and Sofia identified quantum computers as a natural platform to test the validity of Jarzynski’s equality for many interacting quantum particles. (A quantum computer is a computing device that uses the principles of Quantum Mechanics to perform certain types of calculations at speeds and efficiency levels that are unattainable by classical computers. Quantum computers use quantum bits, or qubits, as the basic unit of information. Hence, any quantum computer is, at its core, a system of interacting quantum particles.) The researchers used the quantum bits of the quantum processor to simulate the behaviour of many quantum particles undergoing nonequilibrium processes, as is desired for an experimental verification of Jarzynski’s equality. They tested this fundamental principle of nature on multiple devices and using different quantum computing platforms. To their surprise, they found that the agreement between theory and quantum simulation was more accurate than originally expected due to the presence of computational errors, which are omnipresent in current quantum computers. The results demonstrate a direct link between certain types of errors that can occur in quantum computations and violations of Jarzynski’s equality, revealing a fascinating connection between quantum computing technology and this fundamental principle of physics.
Dominik Hahn, Maxime Dupont, Markus Schmitt, David J. Luitz, and Marin Bukov, Physical Review X 13, 041023 (2023)
Read moreOne of the most remarkable relations in statistical mechanics is Jarzynski's equality, connecting the irreversible work performed in an arbitrary thermodynamic process with the energy and entropy of the system in thermodynamic equilibrium. Because the system is free to leave the equilibrium state during its evolution, Jarzynski’s equality is a prime example of how equilibrium physics can constrain the outcome of nonequilibrium processes. Remarkably, the familiar Second Law of Thermodynamics – a fundamental principle of physics – follows directly from Jarzynski’s equality. The Second Law is a statement about the average properties of particles in a system undergoing a thermodynamic process, and postulates that heat always flows spontaneously from hotter to colder regions of the system. Intriguingly, Jarzynski’s equality shows that this fundamental law of Thermodynamics can be “violated” in individual realizations of a process (but never on average!).
Despite its fundamental importance, experimental tests of Jarzynski’s equality for classical and quantum systems are extremely challenging, since they require complete control in manipulating and measuring the system. Even more so, a test for many quantum interacting particles was until recently completely missing.
In a new joint study, an international team from the Max Planck Institute for the Physics of Complex Systems, the University of California at Berkeley, the Lawrence Berkeley National Laboratory, the German Cluster of Excellence ML4Q and the Universities of Cologne, Bonn, and Sofia identified quantum computers as a natural platform to test the validity of Jarzynski’s equality for many interacting quantum particles. (A quantum computer is a computing device that uses the principles of Quantum Mechanics to perform certain types of calculations at speeds and efficiency levels that are unattainable by classical computers. Quantum computers use quantum bits, or qubits, as the basic unit of information. Hence, any quantum computer is, at its core, a system of interacting quantum particles.) The researchers used the quantum bits of the quantum processor to simulate the behaviour of many quantum particles undergoing nonequilibrium processes, as is desired for an experimental verification of Jarzynski’s equality. They tested this fundamental principle of nature on multiple devices and using different quantum computing platforms. To their surprise, they found that the agreement between theory and quantum simulation was more accurate than originally expected due to the presence of computational errors, which are omnipresent in current quantum computers. The results demonstrate a direct link between certain types of errors that can occur in quantum computations and violations of Jarzynski’s equality, revealing a fascinating connection between quantum computing technology and this fundamental principle of physics.
Dominik Hahn, Maxime Dupont, Markus Schmitt, David J. Luitz, and Marin Bukov, Physical Review X 13, 041023 (2023)
Publication Highlights
Investigating the impact of a defect basepair on DNA melting
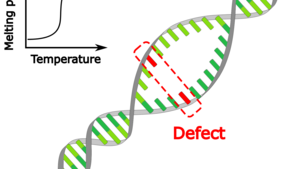
As temperature is increased, the two strands of DNA separate. This DNA melting is described by a powerful model of statistical physics, the Poland–Scheraga model. It is exactly solvable for homogeneous DNA (with only one type of basepairs), and predicts a first-order phase transition.
Arthur Genthon of the Max Planck Institute for the Physics of Complex Systems, Albertas Dvirnas and Tobias Ambjörnsson (Lund University, Sweden) have now derived an exact equilibrium solution of an extended Poland–Scheraga model that describes DNA with a defect site that could, for instance, result from DNA basepair mismatching, cross-linking, or the chemical modifications from attaching fluorescent labels, such as fluorescent-quencher pairs, to DNA. This defect was characterized by a change in the Watson–Crick basepair energy of the defect basepair, and in the associated two stacking (nearest-neighbour) energies for the defect compared to the remaining parts of the DNA. The exact solution yields the probability that the defect basepair and its neighbors are separated at different temperatures. In particular, the authors investigated the impact of the defect on the phase transition, and the number of base pairs away from the defect at which its impact is felt. This work has implications for studies in which fluorophore-quencher pairs are used to analyse single-basepair fluctuations of designed DNA molecules.
Arthur Genthon, Albertas Dvirnas, and Tobias Ambjörnsson, J, Chem. Phys. 159, 145102 (2023)
Read moreArthur Genthon of the Max Planck Institute for the Physics of Complex Systems, Albertas Dvirnas and Tobias Ambjörnsson (Lund University, Sweden) have now derived an exact equilibrium solution of an extended Poland–Scheraga model that describes DNA with a defect site that could, for instance, result from DNA basepair mismatching, cross-linking, or the chemical modifications from attaching fluorescent labels, such as fluorescent-quencher pairs, to DNA. This defect was characterized by a change in the Watson–Crick basepair energy of the defect basepair, and in the associated two stacking (nearest-neighbour) energies for the defect compared to the remaining parts of the DNA. The exact solution yields the probability that the defect basepair and its neighbors are separated at different temperatures. In particular, the authors investigated the impact of the defect on the phase transition, and the number of base pairs away from the defect at which its impact is felt. This work has implications for studies in which fluorophore-quencher pairs are used to analyse single-basepair fluctuations of designed DNA molecules.
Arthur Genthon, Albertas Dvirnas, and Tobias Ambjörnsson, J, Chem. Phys. 159, 145102 (2023)
Publication Highlights
A Quantum Root of Time for Interacting Systems
In 1983, the two physicists Page and Wootters postulated a timeless entangled quantum state of the universe in which time emerges for a subsystem in relation to the rest of the universe. This radical perspective of one quantum system serving as the other’s temporal reference resembles our traditional use of celestial bodies’ relative motion to
track time. However, a vital piece has been missing: the inevitable interaction of physical systems.
Forty years later, Sebastian Gemsheim and Jan M. Rost from the Max Planck Institute for the Physics of Complex Systems have finally shown how a static global state, a solution of the time-independent Schrödinger equation, gives rise to the time-dependent Schrödinger equation for the state of the subsystem once it is separated from its environment to which it retains arbitrary static couplings. Exposing a twofold role, the environment additionally provides a time-dependent effective potential governing the system dynamics, which is intricately encoded in the entanglement of the global state. Since no approximation is required, intriguing applications beyond the question of time are within reach for heavily entangled quantum systems, which are elusive but relevant for processing quantum information.
Sebastian Gemsheim and Jan M. Rost, Phys. Rev. Lett. 131, 140202 (2023)
Read moreForty years later, Sebastian Gemsheim and Jan M. Rost from the Max Planck Institute for the Physics of Complex Systems have finally shown how a static global state, a solution of the time-independent Schrödinger equation, gives rise to the time-dependent Schrödinger equation for the state of the subsystem once it is separated from its environment to which it retains arbitrary static couplings. Exposing a twofold role, the environment additionally provides a time-dependent effective potential governing the system dynamics, which is intricately encoded in the entanglement of the global state. Since no approximation is required, intriguing applications beyond the question of time are within reach for heavily entangled quantum systems, which are elusive but relevant for processing quantum information.
Sebastian Gemsheim and Jan M. Rost, Phys. Rev. Lett. 131, 140202 (2023)
Publication Highlights
Unraveling the mysteries of glassy liquids
When a liquid is cooled to form a glass, its dynamic slows down significantly, resulting in its unique properties. This process, known as “glass transition”, has puzzled scientists for decades. One of its intriguing aspects is the emergence of “dynamical heterogeneities”, when the dynamics become increasingly correlated and intermittent as the liquid cools down and approaches the glass transition temperature.
In a new collaborative study, Ali Tahaei and Marko Popovic from the Max Planck Institute for the Physics of Complex Systems, with colleagues from EPFL Lausanne, ENS Paris, and Université Grenoble Alpes, propose a new theoretical framework to explain the origin of the dynamical heterogeneities in glass-forming liquids.
Based on the premise that relaxation in these materials occurs occurs through local rearrangements of particles that interact via elastic interactions, the researchers formulated a scaling theory that predicts a growing length-scale of dynamical heterogeneties upon decreasing temperature. The proposed mechanism is an example of extremal dynamics that leads to self-organised critical behavior. The proposed scaling theory also accounts for the Stokes-Einstein breakdown, which is a phenomenon observed in glass-forming liquids in which the viscosity becomes uncoupled from the diffusion coefficient. To validate their theoretical predictions, the researchers conducted extensive numerical simulations that confirmed the predictions of the scaling theory.
Ali Tahaei, Giulio Biroli, Misaki Ozawa, Marko Popovic, and Matthieu Wyart, Phys. Rev. X 13, 031034 (2023).
Read moreIn a new collaborative study, Ali Tahaei and Marko Popovic from the Max Planck Institute for the Physics of Complex Systems, with colleagues from EPFL Lausanne, ENS Paris, and Université Grenoble Alpes, propose a new theoretical framework to explain the origin of the dynamical heterogeneities in glass-forming liquids.
Based on the premise that relaxation in these materials occurs occurs through local rearrangements of particles that interact via elastic interactions, the researchers formulated a scaling theory that predicts a growing length-scale of dynamical heterogeneties upon decreasing temperature. The proposed mechanism is an example of extremal dynamics that leads to self-organised critical behavior. The proposed scaling theory also accounts for the Stokes-Einstein breakdown, which is a phenomenon observed in glass-forming liquids in which the viscosity becomes uncoupled from the diffusion coefficient. To validate their theoretical predictions, the researchers conducted extensive numerical simulations that confirmed the predictions of the scaling theory.
Ali Tahaei, Giulio Biroli, Misaki Ozawa, Marko Popovic, and Matthieu Wyart, Phys. Rev. X 13, 031034 (2023).
Publication Highlights
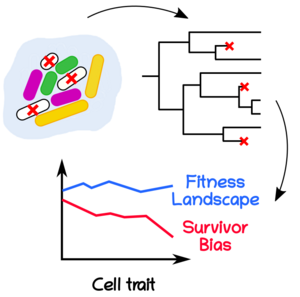
Cell Lineage Statistics with Incomplete Population Trees
Cell lineage statistics is a powerful tool for inferring cellular parameters, such as division rate, death rate, fitness landscape and selection. Yet, in practice such an analysis suffers from a basic problem: how should we treat incomplete lineages that do not survive until the end of the experiment? Examples of such lineages are found in experiments in which cells can die (antibiotic experiments, ...) and in experiments in which cells are diluted to maintain the population constant (microchannels, cytometers, ...).
Arthur Genthon of the Max Planck Institute for the Physics of Complex Systems, Takashi Nozoe (U. Tokyo, Japan), Luca Peliti (Santa Marinella Research Institute, Italy), and David Lacoste (Gulliver, Paris) have now developed a model-independent theoretical framework to address this issue.
They show how to quantify fitness landscape, survivor bias, and selection for arbitrary cell traits from cell lineage statistics in the presence of death, and they test this method using an experimental data set in which a cell population is exposed to a drug that kills a large fraction of the population. This analysis reveals that failing to properly account for dead lineages can lead to misleading fitness estimations. For simple trait dynamics, they prove and illustrate numerically that the fitness landscape and the survivor bias can in addition be used for the nonparametric estimation of the division and death rates, using only lineage histories. Their framework provides universal bounds on the population growth rate, and a fluctuation-response relation that quantifies the change in population growth rate due to the variability in death rate. Further, in the context of cell size control, they obtain generalizations of Powell's relation that link the distributions of generation times with the population growth rate, and they show that the survivor bias can sometimes conceal the adder property, namely the constant increment of volume between birth and division.
Arthur Genthon, Takashi Nozoe, Luca Peliti, and David Lacoste, PRX Life 1, 013014 (2023)
Read moreArthur Genthon, Takashi Nozoe, Luca Peliti, and David Lacoste, PRX Life 1, 013014 (2023)
Publication Highlights
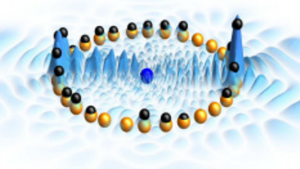
Anderson localization of a Rydberg electron
The hydrogen atom is one of the few exactly solvable quantum systems. Its well-known properties are shared by highly excited Rydberg atoms, albeit to such an exaggerated degree that their behavior is often wholly unexpected.
Scientists at the Max Planck Institute for the Physics of Complex Systems have now investigated a Rydberg atom perturbed by ground state atoms, exploiting hydrogen's infinite spectrum and high degeneracy to show that the Rydberg electron localizes in the same fashion as electrons in a disordered solid. This unexpected manifestation of Anderson localization is enabled by the existence of a well-defined thermodynamic limit of the single Rydberg electron as its principle quantum number and the number of ground state atoms increase in tandem. Myriad localization regimes can be realized as a function of the geometry of the system.
Matthew T. Eiles, Alexander Eisfeld, and Jan M. Rost, Phys. Rev. Research 5, 033032 (2023)
Read moreMatthew T. Eiles, Alexander Eisfeld, and Jan M. Rost, Phys. Rev. Research 5, 033032 (2023)
Publication Highlights
An artificial intelligence agent manipulates many interacting quantum bits of information
In recent years, quantum technologies have experienced significant growth, offering immense potential in various areas. Quantum computers are expected to revolutionise optimisation and search algorithms; quantum simulators help explore new quantum phases of matter; quantum sensors can achieve unparalleled precision in measurements, and quantum cryptography provides robust security for communication protocols. The advantage of these new technologies over their classical counterparts lies in quantum correlations (called by physicists quantum entanglement), and realises phenomena beyond the scope of classical physics.
However, the successful implementation of most quantum technologies relies heavily on the ability to manipulate the underlying quantum systems. This task is already challenging in classical dynamics, but quantum physics adds an extra layer of complexity. The issue arises from the difficulty in simulating quantum systems with many interacting qubits, as the memory requirements exceed the capabilities of even the best classical supercomputers.Physicists refer to this challenge as the "curse of dimensionality", rendering it infeasible to simulate the behavior of large quantum many-body systems using classical computers and devising optimal control strategies for them.
Addressing this problem, Friederike Metz (OIST and EPFL) and Marin Bukov (Max Planck Institute for the Physics of Complex Systems and Sofia University) introduced a new approach: they applied deep reinforcement learning (RL), a subfield of machine learning, to design an artificial intelligent agent capable of controlling quantum many-body systems effectively. To overcome the curse of dimensionality, they employed tensor networks–mathematical structures that allow for an approximate representation of large quantum states on classical computers. Leveraging tensor networks, Metz and Bukov developed a novel deep learning architecture that empowers RL agents to process and interpret quantum many-body states seamlessly.
The trained RL agent demonstrated remarkable performance in preparing ordered ground states in the quantum Ising chain, a fundamental model for studying quantum magnetism. This new framework surpassed the limitations of standard neural-network-only architectures, enabling the control of significantly larger systems while retaining the benefits of deep learning algorithms, such as generalizability and trainable robustness to noise. Notably, the RL agent exhibited the ability to find universal controls in few-qubit systems, learn to steer previously unseen many-qubit states optimally, and adapt control protocols in real-time when faced with stochastic perturbations in quantum dynamics. Additionally, the authors propose a way to map their RL framework to a hybrid quantum-classical algorithm that can be executed on noisy intermediate-scale quantum devices.
This research has profound implications, paving the way for applying deep RL to efficiently control large quantum systems–a crucial requirement for advancing modern quantum technologies. With these techniques, researchers expect to explore novel quantum phases, design complex molecules, achieve unprecedented measurement precision, and build secure networks using quantum communication, among other groundbreaking applications.
An earlier version of this text was improved using ChatGPT. The image accompanying the text was created with the assistance of DALL·E 2 using the prompt "A robot manipulating atoms in a quantum computer, Surrealism".
Friederike Metz and Marin Bukov, Nat. Mach. Intell. 5, 780 (2023)
Read moreHowever, the successful implementation of most quantum technologies relies heavily on the ability to manipulate the underlying quantum systems. This task is already challenging in classical dynamics, but quantum physics adds an extra layer of complexity. The issue arises from the difficulty in simulating quantum systems with many interacting qubits, as the memory requirements exceed the capabilities of even the best classical supercomputers.Physicists refer to this challenge as the "curse of dimensionality", rendering it infeasible to simulate the behavior of large quantum many-body systems using classical computers and devising optimal control strategies for them.
Addressing this problem, Friederike Metz (OIST and EPFL) and Marin Bukov (Max Planck Institute for the Physics of Complex Systems and Sofia University) introduced a new approach: they applied deep reinforcement learning (RL), a subfield of machine learning, to design an artificial intelligent agent capable of controlling quantum many-body systems effectively. To overcome the curse of dimensionality, they employed tensor networks–mathematical structures that allow for an approximate representation of large quantum states on classical computers. Leveraging tensor networks, Metz and Bukov developed a novel deep learning architecture that empowers RL agents to process and interpret quantum many-body states seamlessly.
The trained RL agent demonstrated remarkable performance in preparing ordered ground states in the quantum Ising chain, a fundamental model for studying quantum magnetism. This new framework surpassed the limitations of standard neural-network-only architectures, enabling the control of significantly larger systems while retaining the benefits of deep learning algorithms, such as generalizability and trainable robustness to noise. Notably, the RL agent exhibited the ability to find universal controls in few-qubit systems, learn to steer previously unseen many-qubit states optimally, and adapt control protocols in real-time when faced with stochastic perturbations in quantum dynamics. Additionally, the authors propose a way to map their RL framework to a hybrid quantum-classical algorithm that can be executed on noisy intermediate-scale quantum devices.
This research has profound implications, paving the way for applying deep RL to efficiently control large quantum systems–a crucial requirement for advancing modern quantum technologies. With these techniques, researchers expect to explore novel quantum phases, design complex molecules, achieve unprecedented measurement precision, and build secure networks using quantum communication, among other groundbreaking applications.
An earlier version of this text was improved using ChatGPT. The image accompanying the text was created with the assistance of DALL·E 2 using the prompt "A robot manipulating atoms in a quantum computer, Surrealism".
Friederike Metz and Marin Bukov, Nat. Mach. Intell. 5, 780 (2023)